A bejegyzés első részében betekintettünk a tanuló algoritmusok világába és egy egyszerűbb példán keresztül vizsgáltuk, hogy az ún. "gradient descent" (vagy gradiens) módszer, hogyan alkalmazható egy logisztikus regressziós probléma, a csődvalószínűség modellezése során.
A példában szereplő logisztikus regressziós egyenletünk tulajdonképpen egy nagyon egyszerű, 1 neuronból áll neurális hálózatként is felfogható (ún. perceptron). Ugyanakkor a valódi neurális hálózatok jóval több, rétegekbe rendezett neuronból épülnek fel. Ráadásul az egyes rétegekben levő neuronok közötti kapcsolat erősségének meghatározása - vagyis a hálózat tanítása - a gradiens módszeren alapuló, de ahhoz képest összetettebb algoritmussal, az ún. hiba visszaterjesztés ("error backpropagation") segítségével történik.
A múltkor bemutatott példát továbbgondolva, most egy neurális hálózatot tanítunk meg a csődvalószínűség meghatározására. A bejegyzés következő részében pedig közelebbről is megnézzük a neurális hálózat tanításának lépéseit.
A neurális hálózatunk felépítése
A neurális hálózatok egy bemeneti rétegből, akár több, egymással összeköttetésben álló köztes rétegből és a kimeneti rétegből állnak. Maguk a neuronok matematikai értelemben ún. aktivációs függvények, amelyek a neuronnak a bemeneti adatokra adott “válaszát” képezik le.
A példában szereplő neurális hálózat egy bemeneti rétegből, egy rejtett rétegből és egyetlen neuront tartalmazó kimeneti rétegből áll. Az aktivációs függvény az ún. szigma függvény:
1 / (1 + exp(-inp))
A bemeneti réteg 5 inputot tartalmaz: a standard likviditási ráta, a likviditási gyors ráta, ROE mutató, EBITDA margin értéke és a DEBT/EBITDA mutató (vagyis a korábbi bejegyzésben szereplő példához képest bevezettünk 2 új inputot). A bemeneti értékek közvetlenül a mutatók értékei, semmilyen aktivációs függvénnyel nem “transzformáljuk” azokat.
A köztes réteg 3 neuront tartalmaz, ezek bemeneti jele a pénzügyi mutatók értéke és az aktivációs függvénye által generált jel lesz a kimenetük, amelyek súlyozott értéke egyben a bemeneti réteg egyetlen neuronjának bemenete is.
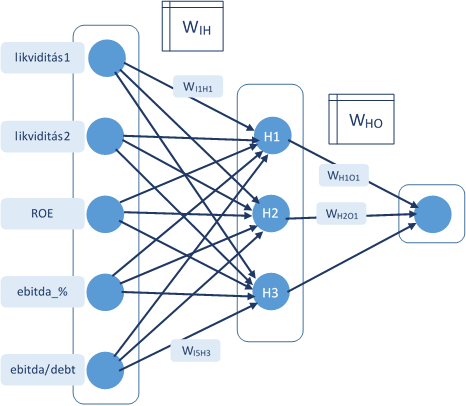
Az egyes rétegek közötti kapcsolatot, vagyis a neuronok közötti összeköttetéseket a súlyokat tartalmazó mátrixok tartalmazzák. Az ábrán látható WIH mátrix például az inputok (I) és a rejtett (Hidden) közötti súlyokat tartalmazza.
Így ez alapján például a rejtett réteg első neuronjának (H1) bemente az alábbi:
Z H1 = Likv1 x WI1H1 + Likv2 x WI2H1 + ROE x WI3H1 + EBITDA_% x WI4H1 + DEBT x WI5H1
A H1 neuron kimenet pedig:
ACT H1 = 1 / (1 + exp(-Z H1))
Az egyes rétegek közötti induló súlyokat véletlenszerűen határozza meg az algoritmusunk az első lépésben, majd ezt követően további 1000 lépésben a hiba visszaterjesztés (backpropagation - ld. következő bejegyzésben) segítségével módosítjuk.
Adatok
A neurális hálózat tanításához 1000 vállalat adatait tartalmazó adathalmazból indultunk ki, de ebből úgy választottunk ki kb. 500 darabot, hogy abban egyenlő arányban legyenek csődbe ment és csődbe nem menő vállalatok.
Az adathalmaz tartalmazza az 5 pénzügyi mutató értékét (bemenő input adatok), valamint a tényleges kimenet értékét (1: csődbe ment; 0: nem ment csődbe).
Kapott eredmény
Az 1000 tanulási ciklust végrehajtó tréning algoritmus során az alábbi súlyokat kaptuk:
Vagyis például a H1 - a rejtett réteg első - neuron bemenetét jelentő input súlya a likviditás1 mutató esetében 1.2158. A kimeneti neuron bemenete és aktivációs függvénye pedig az alábbiak szerint írható fel:
Z O1 = 4.794 - 2.256 x H1 - 6.384 x H2 - 6.069 x H3
ACT O1 = 1 / (1 + exp(-Z O1))
A tanulási folyamat során a neurális hálózat hibája az első kétszáz ciklusban jelentősen csökkent. A 0/1 kimenet alapján a hiba maximális értéke 1 lehet, a véletlenszerűen inicializált súlyok mellett a kezdeti érték 0.6 körüli volt és kb. 200 ciklus után 0.06 körüli szintre csökkent (a további ciklusok során pedig már csak minimális volt a változás).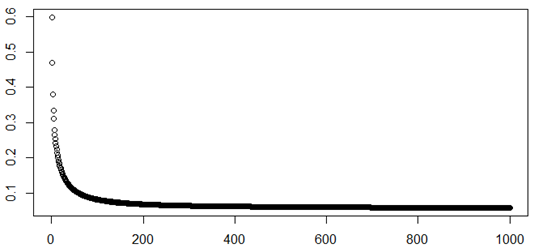
A következő részben megnézzük közelebbről is a tréning algoritmus működését…
